Puzzle Difficulty Levels Explained.
Puzzle difficulty is ranked using the number of deductive steps required to solve the puzzle. Each deductive step consists of one or more logically independent deductions of empty cell values. Each empty cell value can be determined based only on the puzzle information from the previous steps. None of the values deduced in the current step are required to determine other moves in the current step.
Puzzles that are too hard, or too easy, can be one of the most frustrating aspects of puzzle solving for both serious and casual solvers. For this reason, rating puzzles is one of the most important parts of creating Group Puzzles. It is also, however, one of the most difficult. Even apparently simple rating systems, like one to five stars, or "easy," "medium," and "hard," often make assumptions about whether the reader is a serious or casual puzzle solver. The wide variety of Group Puzzles types makes ranking puzzles even more complex. The difficulty ranking system used here is designed to help both casual and serious solvers understand the difficulty of a particular puzzle before attempting a solution.
This difficulty ranking system is not just a simple set of group labels. The "Difficulty Key" or DiffKey is a string of digits and the letters A-D that is derived directly from the deductive solution steps, one character for each step in the solution. The meaning of each character for the step is described in detail in the remainder of this section. The "Difficulty" of a puzzle is just the length of this string, and is, therefore, the number of steps in the deductive solution. This single number provides less information than the DiffKey, but more than a simple rating word. Labels like "Medium" or "Challenging" can then also be used to describe ranges of difficulty levels of puzzles for the purposes of grouping puzzles in book sections. The following names have been chosen for each indicated range of solution steps:
| Difficulty Level: | Number of Deductive Steps |
| Easiest : | 1 or 2 steps |
| Easy: | 3 or 4 steps |
| Medium: | 5 to 8 steps |
| Difficult: | 9 to 14 steps |
| Challenging: | 15 to 20 steps |
| Tournament: | 21 to 29 steps |
| TournamentPlus: | 30 to 45 steps |
| Perplexing: | 46 or more steps |
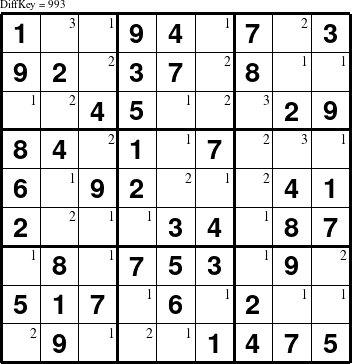
When the character in the DiffKey string for a particular step is a digit from 1 to 8, there are 1 to 8 empty locations that can be deduced directly from just the information given in the puzzle before the step. Thus, a DiffKey of "1" means that the puzzle has only one open empty location, and that location can be filled in based on the information in the puzzle. The digit 9 indicates that nine or more moves are possible in the particular step. Thus, a DiffKey of "9" means that there are nine or more empty locations in the puzzle being rated and that they can all be filled in independently of one another to complete the puzzle. The DiffKey of "993" computed for the puzzle in the indicated figure means that there are two different groups of nine or more empty locations and that, once the first group (marked with a 1 in the upper right corner) that can be deduced directly from the puzzle are filled in, the second group of empty locations (marked with a 2) can all be figured out. The 3 at the end of the DiffKey refers to the last three empty cells that cannot be filled in without first filling in some of the ones marked as 2.
Note, however, that some of the second group can often be deduced once some of the first group are found, but all of the second cannot generally be completed until all of the first are done. Conversely, a DiffKey that begins "112..." means that there is only one empty location in the given puzzle that can be filled in deductively by this algorithm, and once that single filled in location is deduced, one more empty location can be figured out and filled in, but then two additional moves can be determined using both of those filled in locations, etc.
Moves within a step are deduced by the software using one of two methods. The first method works by eliminating all of the other locations within a group for a particular value, i.e., " The only spot left for a 5 in row N is ..." This method is always tried first for a step and if there are 1 to 8 possible moves using this method, the corresponding digit between 1 to 8 is added to the DiffKey; if there are nine or more moves, a 9 is added to the key for the step.
The second method is only used when no deductions are possible using the first method. This method deduces the value for a location by checking if all other possible values for the location already exist in one or more of the other groups (such as a row or column) that include the location, i.e., " 5 must be place at (X, Y) because it is the only value left that is not in the 1st column, 6th row, or ..." The letter A is added to the DiffKey if there is only one move of this type possible at that step. B is used if there are two possible moves of this type, and so on, with D representing 4 or more possible moves.
A quick glance at a DiffKey gives a lot of information about the solution. Puzzles are simpler to solve when there are fewer steps ( i.e., the DiffKey is shorter). Puzzles are also simpler to solve when there are more moves within each step. For example, a DiffKey that begins "999975" indicates that there are many moves available in each of the first four steps before moves become more restricted in the subsequent two steps. The simplest puzzles have short DiffKey values of all 9s. The most difficult puzzles have long strings of low value digits, from 1 to 3 or so, that indicate deductive bottlenecks. Moves that use deductive method 1, and are represented with digits in the DiffKey, are typically easier for most people to find than deductive moves found using method 2, which are represented using the letters A-D.
There exist many other possible deductive methods to solve Sudoku-like Group Puzzles beyond the two used to construct DiffKeys. Indeed, the only method that is guaranteed to eventually solve all possible puzzles that can be solved ( i.e., they have a single unique solution), is the non-deterministic guess-and-check method with backtracking. Puzzles without deterministic deductive solutions, however, are typically much harder to solve (at least for humans) and can take much more time (for computers and humans alike) because each guess requires backtracking to the point of the guess if a logical inconsistency is ever encountered after the guess. An asterisk, "*" is added to the DiffKey if neither of the deterministic methods yields a solution and a guess is required to solve the puzzle. The DiffKey algorithm currently rates the puzzle as having no solution DiffKey if a solution cannot be found that requires only a single guess. For this reason, a DiffKey will not contain more than one asterisk. The DiffKey puzzle rating system may be extended in the future to include specific types of non-deterministic steps, as well as other types of deductive deterministic reasoning steps, by defining additional character codes for DiffKey strings which indicate that these types of steps are required at that particular point in the solution.