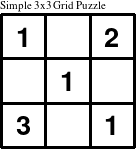Logic Practice?
Everyone understands and encourages long hours of practice for sports, music, and many other endeavors. Logic should be no different. No one doubts that Olympic athletes and professional sports stars practice their craft constantly in spite of their obvious talents. Moreover, many motivational books and lectures often focus on the life story of someone who has "made it" in their chosen field through hard work and determination in spite of abilities that do not make them stand out among their peers. Ask someone to practice thinking ... Or worse, practice logic ... Suddenly all of those lessons do not seem to apply, even though most of life's challenges come from making important decisions off the field and require most of all, the ability to think clearly.
Many people, especially those that enjoy working puzzles of any type, believe that practice does make one a stronger and more agile thinker (to use the sports metaphor) and that such abilities do carry over to the rest of life. Many start every morning with a puzzle as a type of mental calisthenics to get "warmed up. " Moreover, education research has shown that active mental exercises, even simple ones like reading a book, have a more positive impact on learning than passive activities, such as watching videos. Puzzles of any sort, therefore, offer an even greater opportunity to exercise your mind because they require a more active involvement in the material than reading. Just as word puzzles can exercise verbal skills and math puzzles can exercise math skills, logic puzzles exercise logic and deductive reasoning skills that can help lead to clear-minded decision making.
Unfortunately, even some ardent puzzle lovers have found Sudoku-type Group Puzzles too hard or difficult, and in the final analysis, simply not fun. Starting a brief survey of why these people did not work group logic puzzles, such as Sudoku, quickly revealed what should have been obvious: most puzzles are published for those people who already know and love group logic puzzles. Even puzzles marked as "Easy" in newspapers and magazines can prove daunting to someone who has never worked such a puzzle unless they have someone available to tutor them briefly about the basics. At the very least, they need step-by-step solutions to puzzles describing how someone can deductively reason from the particular puzzle that they are currently working on to the completed grid. The answer grid published with most Sudoku puzzles as puzzle solutions, in contrast, only tells you whether you have arrived, not how to get there. Although we do not expect students to learn a subject like math from just a set of problems and answers, with no explanation, tutoring, or step-by-step solutions, most sources of logic puzzles do exactly this. Thus, these publications limit their audience to those who already know and like such puzzles and, more importantly, limit their usefulness in teaching logic in an educational environment.
Teaching Logic and Deduction.
For many people who enjoy working logic puzzles it is simply "obvious" that puzzles are a good tool for teaching logic, and nothing further needs to be said. For people who enjoy these puzzles and understand how to work them, that is true. For many others, however, especially for children and those who teach them, there are a number of challenges and potential pitfalls facing the use of puzzles to teach logic in the general population and in schools.
Purely Deductive Puzzles.
Teaching logic is difficult. Teaching guessing is unnecessary. In order to teach logic using Group Puzzles, like traditional Sudoku puzzles, there must be at least one purely deductive set of steps that shows how to logically get from every puzzle to its answer grid that requires no guessing or backtracking. Students must know that the easiest way to solve the puzzle is to use logic so that they actively and habitually look for solutions that are deductive. Purely deductive solutions for other published Sudoku puzzles may exist, but such solutions are rarely guaranteed. This is one barrier to the effective use of existing puzzle sources to teach logic. Another barrier to this use of puzzles is the lack of availability of step-by-step deductive solutions. Detailed step-by-step instructions are required not only for instructors who wish to use puzzles, but may not have the time to work each puzzle before the students, but also for anyone who has never worked such a puzzle and wishes to teach themselves. Existing publishers for Sudoku puzzles do not provide step-by-step instructions that describe what values can be placed where in a puzzle, and why. Indeed, a number of puzzles in some publications have been found to have no simple deductive solution and require guessing and backtracking. These are usually "symmetric" puzzles, so named because they are constructed from a solution grid using a pattern of empty cells that is reflectively symmetric about one or more axes. Symmetric puzzles are an attempt to approximate puzzle difficulty by use of these patterns. When puzzles are rated quantitatively, however, symmetric puzzles have been found to provide only a coarse probabilistic approximation to puzzle difficulty in terms of the number of deductive steps required to solve the puzzle.
Guaranteed Correct Puzzles.
Like any other educational tool, the effectiveness of using puzzles to teach logic requires educational materials, including puzzles, strategy guides, step-by-step solutions, and hints, that are always correct. Incorrect puzzles teach students that logic and deduction do not work. Incorrect puzzles teach students to guess rather than to reason and solve. Incorrect puzzles drive students away from logic. Students must know that the effort expended in logically deducing solutions is not a wasted effort or the puzzles are no longer fun and become just another school chore. Puzzle correctness can be guaranteed by the use of a set of automated tools and stringent quality control measures that eliminate errors in the puzzle generation, rating, and type setting processes.
Carefully Calibrated Puzzle Difficulty.
The educational effectiveness of puzzles is also strongly dependent on matching puzzle difficulty to the solver's current abilities. Puzzles that are too hard make students frustrated and risk the most important advantage they have for teaching: making learning fun. Puzzles that are too simple have little teaching value or make students bored, also risking the fun factor. Thus, educational logic puzzles require a very accurate puzzle difficulty rating system. This, however, is yet another barrier to the effective use of existing puzzle sources. Most publishers separate puzzles into sections with labels, such as Easy, Medium, and Hard. The detailed quantitative classification algorithm described here, however, has been used to show that there is tremendous overlap in the difficulty ratings in sections of some existing publications with supposedly different difficulty classifications. Indeed, in one publication there were puzzles that required guessing (i.e. they were nondeterministic) in the section labeled "medium" rather than in the section labeled "hard," although there were fewer nondeterministic puzzles in that section. In addition, the puzzle with the most difficult deterministic solution in the entire book was found in the medium section, not the hard section.
Diverse Puzzle Difficulty Levels.
Carefully calibrated puzzle difficulty is only as effective as the availability of puzzles at a wide variety of difficulty levels. Working puzzles provides vital practice of logic skills, but these skills must be exercised regularly and the exercise itself must be well-suited to each person's current ability level so that they are challenged without being overwhelmed. This requires puzzles at many difficulty levels, from very simple to extremely challenging, for puzzles of every type. The easy availability of puzzles at the appropriate level of difficulty helps students make steady progress without risking frustration or boredom.
Diverse Logic Puzzle Types.
There are several reasons why many different types of logic puzzles are essential to teaching logic. First, new and different puzzle types help to keep and hold the interest of students. If they are not fun, then one of the key advantage of puzzles is lost. Second, smaller puzzles are inherently easier to work than larger puzzles and choosing the type of puzzle is the first and most important part of selecting the appropriate difficulty of a puzzle for a particular audience. A simple 3x3 grid puzzle, such as the one shown here,
may prove challenging for most younger children, but boring and unappealing to older grades. Larger Group Puzzles (such as 12 or 16) also greatly increase the difficulty of a puzzle, more so than just the overall size. For example, a 12x12 grid with 12 distinct group values and an overall size of 144 cells can be much more difficult than one of the Sunday newspaper puzzles with five overlapping traditional Sudoku puzzle with 9 distinct group values on a 21x21 grid with an overall size of 369 cells. Third, and perhaps most importantly, new types of puzzles help students generalize their solving techniques and logic skills rather than focusing on the puzzles themselves and developing mental habits that are useful only in solving one particular type of puzzle, such as the traditional Sudoku puzzle. Since group logic puzzle are mathematical constraint satisfaction problems, there is no simple algorithm to deductively solve all such puzzles, so children can (and should) be encouraged to discover their own puzzle solving rules and heuristics and then check them for correctness and usefulness by applying them to new puzzles. Since the rules for checking solutions to these puzzle are simple enough that even young children can understand the rules of the smaller puzzles, Group Puzzles offer a wonderful opportunity to combine both logic and fun for everyone.
Puzzles Annotated with Step Numbers.
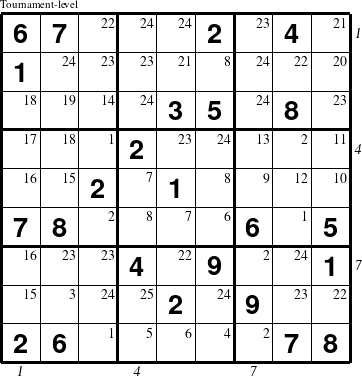
Another way to focus on learning logic is to solve one of the harder or larger puzzles using a grid that shows the step in which each empty cell can be deduced using the rules outlined in the general strategy guide. Knowing which cells can be filled in given the current state of the puzzle is often the hardest part of finding a solution. Specifying that information in the puzzle itself eliminates the question of where to work on the puzzle next and allows the solver to focus on looking for a specific solution using only logic, since they know there has to be a way for the value of the cells in the current step to be deduced from the given information. While this approach can be used for any puzzle type and any difficulty level, it is particularly useful for very large or very difficult puzzles where there are many more options to consider that lead to a solution. For example, in the tournament-level puzzle shown here, there are 25 dependent steps that lead to the solution using the standard algorithm.
The step number is annotated in the top right corner of each empty cell. All cells with the same number can be logically deduced independently of one another from only the initial givens and all the cells with lower step numbers. Using these types of puzzles annotated with the solution step information can change the problem solving experience significantly because the frustration associated with fruitlessly searching for the next move can be avoided for those that have not yet acquired those skills. Thus, these types of puzzles with step numbers annotated in all the empty cells are, in a very real sense, a new type of puzzle in and of themselves.
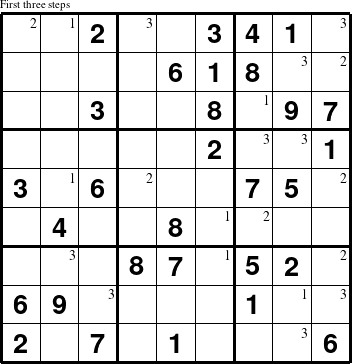
Another variation on this type of puzzle is to fill in some, but not all, of the step numbers on the harder or larger puzzles. For example, annotating the first several steps of puzzles provides the opportunity for solvers to tackle harder puzzles than they usually attempt.
Annotating the last few steps is another possible variation that outlines to the solver the more difficult areas of the puzzle to help them avoid wasting effort, without providing them with an explicit road map of how to go about solving the puzzle.
The beauty of these types of puzzles is that there are an enormous number of logical ways to solve each puzzle and many different heuristics and strategies for each solver to discover, practice, and evaluate. The key is to enable this type of learning without limiting future opportunities for additional learning, by providing a wide variety of puzzles and only general guidance.